平成24年春期試験問題 午前Ⅱ 問3
問3解説へ
COCOMOにはシステム開発の工数を見積もる式の一つに
MM=3.0×(KDSI)1.12
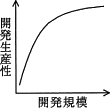
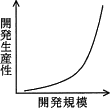
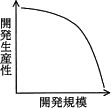
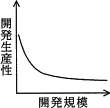
がある。開発規模(KDSI)と開発生産性(KDSI/MM)の関係を表したグラフはどれか。ここで,MMは開発工数(人月),KDSIは開発規模(注釈を除いたソースコードの行数,単位はk行)である。
MM=3.0×(KDSI)1.12
がある。開発規模(KDSI)と開発生産性(KDSI/MM)の関係を表したグラフはどれか。ここで,MMは開発工数(人月),KDSIは開発規模(注釈を除いたソースコードの行数,単位はk行)である。
正解 エ問題へ
分野:マネジメント系
中分類:プロジェクトマネジメント
小分類:プロジェクトのコスト
中分類:プロジェクトマネジメント
小分類:プロジェクトのコスト
広告
解説
スマートな解き方ではありませんが、KDSIに何通りか仮の値を代入して開発生産性(KDSI/MM)の推移を確認するのが確実な方法だと思います。
下表は開発規模と開発生産性の関係を表したものです。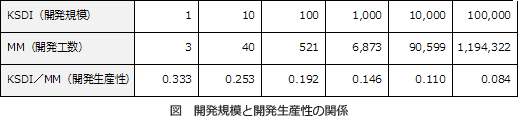 これを見るとKDSI(開発規模)が大きくなるほど、MM(開発工数)は右肩上がりに増加していきます。KDSI/MM(開発生産性)は、それに伴い下がっていきますが、KDSIの増加度合と比較すると、漸近線のような緩やかな曲線を描いて減少していくことがわかります。
これを見るとKDSI(開発規模)が大きくなるほど、MM(開発工数)は右肩上がりに増加していきます。KDSI/MM(開発生産性)は、それに伴い下がっていきますが、KDSIの増加度合と比較すると、漸近線のような緩やかな曲線を描いて減少していくことがわかります。
したがって、2要素の関係を正しく表わしているのは「エ」のグラフになります。
【別解】
以下は掲示板にご投稿いただいた別の解き方です。
グラフは、x軸が開発規模、y軸が開発規模/開発工数ですので、この曲線の式は次のように表すことができます。
y=開発規模3.0×開発規模1.12=x3.0×x1.12≒0.33×1x0.12
x0.12は、xの0.12乗であり、xのおよそ8乗根です。xの8乗根は、x=1のときに1、x=1億のときに10、x=1億の2乗のときに100というように、xの増え方に比較してかなりゆっくりな増え方です(選択肢「ア」の形)。
そうすると、y=0.33×1xという反比例のグラフ(下に凸)をベースにして、xが大きくなればなるほど、yはゆっくりと減少しますから、「エ」の形状になることがわかります。
下表は開発規模と開発生産性の関係を表したものです。

したがって、2要素の関係を正しく表わしているのは「エ」のグラフになります。
【別解】
以下は掲示板にご投稿いただいた別の解き方です。
グラフは、x軸が開発規模、y軸が開発規模/開発工数ですので、この曲線の式は次のように表すことができます。
y=開発規模3.0×開発規模1.12=x3.0×x1.12≒0.33×1x0.12
x0.12は、xの0.12乗であり、xのおよそ8乗根です。xの8乗根は、x=1のときに1、x=1億のときに10、x=1億の2乗のときに100というように、xの増え方に比較してかなりゆっくりな増え方です(選択肢「ア」の形)。
そうすると、y=0.33×1xという反比例のグラフ(下に凸)をベースにして、xが大きくなればなるほど、yはゆっくりと減少しますから、「エ」の形状になることがわかります。
広告